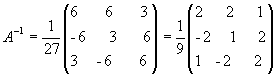Jak získat nezletilého?

V tomto tématu se budeme zabývat pojmy algebraický doplněk a moll. Prezentace materiálu vychází z pojmů vysvětlených v tématu „Matrice. Typy matic. Základní pojmy“. Budeme také potřebovat nějaké vzorce pro výpočet determinantů. Vzhledem k tomu, že toto téma obsahuje mnoho pojmů souvisejících s nezletilými a algebraickými doplňky, přidám stručné shrnutí pro snazší orientaci v materiálu.

Vedlejší (M_) prvku (a_)

Nechť je dána čtvercová matice (A_) (tj. čtvercová matice n-tého řádu).

matice (A_) pojmenovávají determinant matice získaný z matice (A) vymazáním i-tého řádku a j-tého sloupce (tj. řádku a sloupce, na jejichž průsečíku se prvek (a_) nachází).

Uvažujme například čtvercovou matici čtvrtého řádu: (A=left( začátek 1 & 0 & -3 & 9 2 & -7 & 11 & 5 -9 & 4 & 25 & 84 3 & 12 & -5 & 58 konec vpravo)). Najdeme moll prvku (a_), tzn. najdeme (M_). Nejprve si zapišme moll (M_) a potom vypočítejme jeho hodnotu. Abychom mohli skládat (M_), vymažeme z matice (A) třetí řádek a druhý sloupec (prvek (a_) se nachází na průsečíku třetího řádku a druhého sloupce). Získáme novou matici, jejímž determinantem je požadovaná vedlejší (M_):

Tuto minoritu lze snadno vypočítat pomocí vzorce č. 2 z tématu Výpočet determinantů druhého a třetího řádu:

[ M_=vlevo| začátek 32 & -1 & 3 9 & 2 & 11 5 & -3 & 5 konec vpravo|= 58cdot 1cdot 11+(-58)cdot 3cdot 5+3cdot (-2)cdot 5-9cdot 9cdot 11-(- 3) cdot 3cdot 2-58cdot (-5)cdot 5=1. ]

Takže vedlejší prvek (a_) je 579, tj. (M_=579).

Často se v literatuře místo fráze „maticový prvek minor“ vyskytuje „determinant element minor“. Podstata zůstává stejná: pro získání moll prvku (a_) je třeba škrtnout i-tý řádek a j-tý sloupec z původního determinantu. Zbývající prvky jsou zapsány do nového determinantu, kterým je moll prvku (a_). Nalezněme například vedlejší prvek (a_) determinantu (levý| začátek -1 & 3 & 2 9 & 0 & -5 4 & -3 & 7 konec pravý|). Abychom mohli zapsat požadovanou vedlejší (M_), musíme proškrtnout první řádek a druhý sloupec z daného determinantu:

Pro zjištění hodnoty této minority použijeme vzorec č. 1 z tématu Výpočet determinantů druhého a třetího řádu:

[ M_=vlevo| začátek 12 & -9 5 & 4 konec vpravo|=7cdot 9-(-7)cdot 5=4. ]

Takže vedlejší prvek (a_) je 83, tj. (M_=83).

Algebraický doplněk (A_) prvku (a_)

Nechť je dána čtvercová matice (A_) (tj. čtvercová matice n-tého řádu).

(A_) prvek (a_) matice (A_) najdeme podle následujícího vzorce:

kde (M_) je minorita prvku (a_).

Pojďme najít algebraický doplněk prvku (a_) matice (A=left( začátek 1 & 0 & -3 & 9 2 & -7 & 11 & 5 -9 & 4 & 25 & 84 3 & 12 & -5 & 58 konec vpravo)), tzn. najdeme (A_). Již jsme našli vedlejší (M_=579), takže použijeme získaný výsledek:

Obvykle se při hledání algebraických doplňků nepočítá samostatně vedlejší a teprve potom doplněk samotný. Drobná poznámka je vynechána. Například najdeme (A_), jestliže (A=left( začátek -5 & 10 & 2 6 & 9 & -4 4 & -3 & 1 konec vpravo)). Podle vzorce (A_=(-1)^cdot M_=-M_). K získání (M_) však stačí proškrtnout první řádek a druhý sloupec matice (A), proč tedy zavádět extra zápis pro moll? Okamžitě si zapišme výraz pro algebraický doplněk (A_):

Minor k-tého řádu matice (A_)

Jestliže jsme v předchozích dvou odstavcích mluvili pouze o čtvercových maticích, pak zde budeme hovořit i o pravoúhlých maticích, u kterých se počet řádků nemusí nutně rovnat počtu sloupců. Nechť je tedy dána matice (A_), tzn. matice obsahující m řádků a n sloupců.

matice (A_) je determinant, jehož prvky jsou umístěny v průsečíku k řádků a k sloupců matice (A) (předpokládá se, že (k≤ m) a (k≤ n)).

Zvažte například tuto matici:

[A=left( začít -1 & 0 & -3 & 9 2 & 7 & 14 & 6 15 & -27 & 18 & 31 0 & 1 & 19 & 8 0 & -12 & 20 & 14 5 & 3 & -21 & 9 23 & -10 & -5 & 58 konec že jo) ]

Napišme k tomu nějaký vedlejší třetí řád. Abychom mohli napsat moll třetího řádu, musíme vybrat libovolné tři řádky a tři sloupce této matice. Například vezměte řádky č. 2, č. 4, č. 6 a sloupce č. 1, č. 2, č. 4. Na průsečíku těchto řádků a sloupců budou umístěny prvky požadované vedlejší položky. Na obrázku jsou vedlejší prvky zobrazeny modře:

Nezletilí prvního řádu se nacházejí na průsečíku jednoho řádku a jednoho sloupce, tzn. minority prvního řádu se rovnají prvkům dané matice.

Vedlejší prvek k-tého řádu matice (A_=(a_)) se nazývá, pokud na hlavní diagonále této vedlejší matice jsou pouze hlavní diagonální prvky matice (A).

Dovolte mi připomenout, že prvky matice, jejichž indexy jsou stejné, se nazývají: (a_), (a_), (a_) a tak dále. Například pro matici (A) uvažovanou výše budou takové prvky (a_=-1), (a_=7), (a_=18), (a_=8). Na obrázku jsou zvýrazněny zeleně:

[vlevo( začít tučnězelená & 0 & -3 & 9 2 & tučně zelená & 14 & 6 15 & -27 & tučně zelená & 31 0 & 1 & 19 & tučně zelená 0 & -12 & 20 & 14 5 & 3 & -21 & 9 23 & -10 & -5 & 58 konec že jo) ]

Pokud například v matici (A) přeškrtneme řádky a sloupce očíslované 1 a 3, pak v jejich průsečíku budou prvky moll druhého řádu, na jejíž hlavní diagonále budou pouze diagonální prvky matice (A) (matice prvků (a_=-1) a (a_=18) (A)). Dostaneme tedy hlavní moll druhého řádu:

[ M=left|začít tučně zelený & -315 & tučně zelený konec vpravo| ]

Přirozeně bychom mohli vzít jiné řádky a sloupce, například s čísly 2 a 4, čímž bychom získali jinou hlavní moll druhého řádu.

Nechť nějaký moll (M) k-tého řádu matice (A_) není roven nule, tzn. (Mneq 0). V tomto případě jsou všichni nezletilí, jejichž řád je vyšší než k, roven nule. Potom se nazývá moll (M) a řádky a sloupce, na kterých jsou umístěny prvky základního mollového, se nazývají a .

Zvažte například následující matici:

[A=left( začít -1 & 0 & 3 & 0 & 0 2 & 0 & 4 & 1 & 0 1 & 0 & -2 & -1 & 0 0 & 0 & 0 & 0 & 0 konec že jo) ]

Zapišme si moll této matice, jejíž prvky se nacházejí na průsečíku řádků č. 1, č. 2, č. 3 a sloupců č. 1, č. 3, č. 4. Dostaneme moll třetího řádu (jeho prvky jsou v matici (A) zvýrazněny fialově):

Hodnotu této moll najdeme pomocí vzorce č. 2 z tématu Výpočet determinantů druhého a třetího řádu:

[M=vlevo| začít -1 & 3 & 0 2 & 4 & 1 1 & -2 & -1 konec right|=4+3+6-2=11. ]

Takže (M=llneq 11). Nyní zkusme sestavit libovolný moll, jehož pořadí je vyšší než tři. Abychom vytvořili moll čtvrtého řádu, musíme použít čtvrtý řádek, ale všechny prvky tohoto řádku jsou nulové. Proto bude mít každý moll čtvrtého řádu nulový řádek, což znamená, že všechny nezletilé čtvrtého řádu se rovnají nule. Nemůžeme vytvářet minory pátých a vyšších řádů, protože matice (A) má pouze 0 řádky.

Našli jsme moll třetího řádu, který se nerovná nule. V tomto případě jsou všechny nezletilé vyšších řádů rovny nule, proto je nezletilý, který jsme uvažovali, základní. Řádky matice (A), na kterých jsou umístěny prvky této vedlejší (první, druhý a třetí), jsou základními řádky a první, třetí a čtvrtý sloupec matice (A) jsou základními sloupci.

Tento příklad je samozřejmě triviální, protože jeho účelem je jasně ukázat podstatu základní moll. Obecně může existovat několik základních nezletilých a obvykle je proces hledání takového nezletilého mnohem složitější a rozsáhlejší.

Představme si další pojem – hraniční moll.

Nechť určitý k-tý řád menší (M) matice (A_) leží v průsečíku k řádků a k sloupců. K množině těchto řádků a sloupců přidáme další řádek a sloupec. Výsledná moll (k+1) řádu se nazývá moll (M).

Podívejme se například na následující matici:

[A=left( začít -1 & 2 & 0 & -2 & -14 3 & -17 & -3 & 19 & 29 5 & -6 & 8 & -9 & 41 -5 & 11 & 19 & -20 & -98 6 & 12 & 20 & 21 & 54 -7 & 10 & 14 & -36 & 79 konec že jo) ]

Napišme moll 2. řádu, jehož prvky se nacházejí na průsečíku řad č. 5 a č. 2 a také sloupců č. 4 a č. XNUMX. Tyto prvky jsou v matici zvýrazněny červeně:

K množině řádků, na kterých leží prvky vedlejší (M), přidáme další řádek č. 1 a k množině sloupců sloupec č. 5. Získáme novou moll (M’) (již třetího řádu), jejíž prvky se nacházejí na průsečíku řad č. 1, č. 2, č. 5 a sloupců č. 2, č. 4, č. 5. Prvky moll (M) na obrázku jsou zvýrazněny červeně a prvky, které přidáme k mollovi (M), jsou zvýrazněny modře:

Minor (M’) je hraniční moll pro moll (M). Podobně přidáním řádku č. 4 k množině řádků, na kterých leží prvky moll (M) a sloupce č. 3 k množině sloupců, získáme vedlejší (M) (moll třetího řádu):

Minor (M”) je také hraniční moll pro moll (M).

Minor k-tého řádu matice (A_). Další vedlejší. Algebraický doplněk k moll čtvercové matice.

Vraťme se znovu ke čtvercovým maticím. Představme si pojem doplňkové nezletilé.

Nechť je dán určitý moll (M) k-tého řádu matice (A_). Determinant (n-k)-tého řádu, jehož prvky jsou získány z matice (A) po smazání řádků a sloupců obsahujících minoritní položku (M), se nazývá vedlejší (M).

Uvažujme například čtvercovou matici pátého řádu:

[ A=left(začátek -1 & 2 & 0 & -2 & -14 3 & -17 & -3 & 19 & 29 5 & -6 & 8 & -9 & 41 -5 & 11 & 16 & -20 & -98 -7 & 10 & 14 & -36 & 79 konec že jo) ]

Vyberme řádky č. 1 a č. 3 a také sloupce č. 2 a č. 5. Na průsečíku těchto řádků a sloupců budou vedlejší prvky (M) druhého řádu. Tyto prvky jsou v matici (A) zvýrazněny zeleně:

Nyní odejmeme z matice (A) řádky č. 1 a č. 3 a sloupce č. 2 a č. 5, na jejichž průsečíku jsou prvky vedlejší (M) (prvky odebraných řádků a sloupců jsou na obrázku níže zobrazeny červeně). Zbývající prvky tvoří moll (M):

Vedlejší moll (M’), jehož pořadí je (5-2=3), je komplementární moll k moll (M).

(M) čtvercové matice (A_) se nazývá výraz ((-1)^cdot M’), kde (alfa) je součet čísel řádků a sloupců matice (A), na které jsou prvky matice moll (M) jsou umístěny a (M’) – moll, komplementární k moll (M).

Fráze „algebraický doplněk k moll (M)“ je často nahrazena frází „algebraický doplněk k moll (M)“.

Uvažujme například matici (A), pro kterou jsme našli moll druhého řádu ( M=left| začátek 2 & -14 -6 & 41 konec pravý| ) a další moll třetího řádu: (M’= vlevo| začátek 3 & -3 & 19 -5 & 16 & -20 -7 & 14 & -36 konec vpravo|). Označme algebraický doplněk moll (M) jako (M^*). Pak podle definice:

Parametr (alfa) je roven součtu počtu řádků a sloupců, na kterých se nachází vedlejší (M). Tato vedlejší se nachází na průsečíku řad č. 1, č. 3 a sloupců č. 2, č. 5. Proto (alfa=1+3+2+5=11). Tak:

[ M^*=(-1)^cdot M’=-left| začátek 11 & -3 & 3 -19 & 5 & -16 -20 & 7 & -14 konec vpravo|. ]

V zásadě pomocí vzorce č. 2 z tématu Výpočet determinantů druhého a třetího řádu můžete dokončit výpočty a získat hodnotu (M^*):

[ M^*=-vlevo| začít 3 & -3 & 19 -5 & 16 & -20 -7 & 14 & -36 konec vpravo|=-30. ]
Návrat na seznam témat
Zeptejte se na fóru
Přihlaste se na kurzy

Všimli jste si chyby, překlepu nebo byl vzorec zobrazen nesprávně? Napište prosím do tohoto vlákna na fóru.

Pokud máte nějaké návrhy, zpětnou vazbu nebo připomínky týkající se zveřejněných materiálů, můžete o nich napsat v tomto tématu. Není nutná žádná registrace.

Programování se nedá naučit, dá se jen naučit

Matrix nezletilí
Nechť je dána čtvercová matice A, n-tého řádu. Menšina některého prvku aij, determinant matice n-tého řádu, je determinant (n – 1)-tého řádu, získaný z původního přeškrtnutím řádku a sloupce, na jehož průsečíku je vybraný prvek. aij se nachází. Označuje Mij.
Podívejme se na příklad determinantu matice 3 – jeho pořadí:

, pak podle definice minoru bude determinantem vedlejší M12 odpovídající prvku a12:

Zároveň si s pomocí nezletilých můžete zjednodušit úkol výpočtu determinantu matice. Je nutné rozšířit determinant matice po určitém řádku a pak bude determinant roven součtu všech prvků tohoto řádku na jejich vedlejší. Rozklad determinantu matice 3 – její pořadí bude vypadat takto:

, znaménko před součinem je (-1)n, kde n = i + j.

Algebraické sčítání:
Algebraický doplněk prvku determinant se nazývá výraz ve tvaru: = Kde prvek moll .
Poté můžeme přeformulovat výše uvedenou vlastnost.
Determinant matice se rovná součtu součinů prvků určitého řádku (řádku nebo sloupce) matice jejich odpovídajícími algebraickými doplňky.
příklad. Algebraický doplněk prvku :
= =

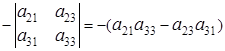
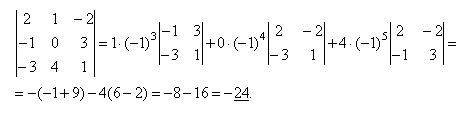
příklad:

Nesingulární matice je čtvercová matice, jejíž determinant se nerovná nule.
Singulární matice je čtvercová matice, jejíž determinant je 0.

Výpočet determinantu
Determinant lze vypočítat jeho rozšířením přes libovolný řádek (sloupec) následovně,
podle řádku: 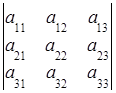= ++, (=1,2,3);

podle sloupce: 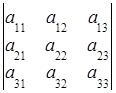= ++, (= 1,2,3).

Příklad. Rozšíření determinantu v prvním řádku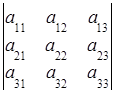
= ++;
= = ; = = ;
= = ;
=.

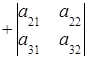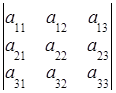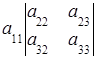
Příklad. Výpočet determinantu rozšířením na první řádek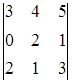
= = ;
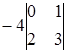
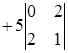Podobně lze tento determinant rozšířit přes kterýkoli jiný řádek (sloupec).

inverzní matice
matice nazývá se inverzí matice , pokud = = Kde je matice identity.
Každá nesingulární matice má inverzní matici a navíc pouze jednu, tzn. Aby čtvercová matice A měla inverzní matici, je nutné a postačující, aby její determinant byl odlišný od nuly.
Chcete-li získat inverzní matici, použijte vzorec:

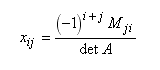
, kde Mji je další vedlejší prvek prvku aji matice A.
Vlastnosti inverzních matic:

1. (A-1)-1 = A;
2. (AB)-1 = B-1A-1;
3. (AT)-1 = (A-1)T;

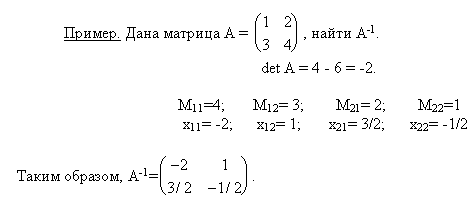
příklad. Pro matici A najděte inverzní.

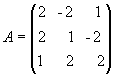
rozhodnutí. Nejprve najdeme determinant matice A

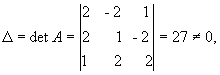
To znamená, že existuje inverzní matice.





odkud