Pojem filtrování se v elektrotechnice používá k označení toho aspektu zpracování signálu, který se týká odstranění nežádoucích složek, jako je šum, ze signálu.
Před nástupem digitální techniky, zejména digitálních počítačů, se filtrování provádělo výhradně prostřednictvím elektrických obvodů nebo zařízení zvaných filtry. Mohou být lineární nebo nelineární v závislosti na typu obvodů nebo zařízení (lineárních nebo nelineárních), ze kterých jsou konstruovány.
Průmyslové zdroje energie poskytují téměř sinusové průběhy napětí. Současně se v řadě případů střídavé proudy a napětí, které jsou periodické, výrazně liší od harmonických.
Elektrické filtry lze použít k vyhlazení zvlnění napětí v usměrňovačích, demodulátorech, které převádějí amplitudově modulované vysokofrekvenční oscilace na relativně pomalé změny napětí signálu, a dalších podobných zařízeních.
V nejjednodušším případě se můžeme omezit na zapojení tlumivky do série se zátěží, jejíž odpor roste s rostoucím harmonickým řádem a je relativně malý pro nízkofrekvenční kmitání a ještě více pro konstantní složku. Efektivnější je použití filtrů ve tvaru U, T a L.

Základní definice a klasifikace elektrických filtrů
Selektivita filtru je jeho schopnost izolovat určitý rozsah frekvencí vlastní užitečnému signálu od celého spektra frekvencí proudů přicházejících na jeho vstup.
Pro získání dobré selektivity musí filtr propouštět proudy s frekvencemi vlastními užitečnému signálu s minimálním útlumem a musí mít maximální útlum pro proudy všech ostatních frekvencí. V souladu s tím může mít filtr následující definici.
Elektrický filtr je čtyřsvorková síť, která propouští proudy v určitém frekvenčním pásmu s mírným útlumem (propustné pásmo) a proudy s frekvencemi mimo toto pásmo s vysokým útlumem, nebo, jak se běžně říká, neprochází (bez propustného pásma) .
Podle struktury obvodů se filtry dělí na řetězové (žebříkové) a můstkové. Řetězové filtry jsou ty, které jsou vyrobeny pomocí můstkových obvodů ve tvaru T, P a L. Můstkové filtry jsou filtry vyrobené pomocí můstkového obvodu.
V závislosti na povaze prvků se filtry dělí na:
- LC – jejichž prvky jsou indukčnost a kapacita;
- RC – jejichž prvky jsou aktivní odpory a kapacity;
- rezonátor – jehož prvky jsou rezonátory.
Na základě přítomnosti zdrojů energie ve filtračním okruhu se dělí na:
- pasivní – neobsahují zdroje energie uvnitř obvodu;
- aktivní – obsahující zdroje energie uvnitř obvodu ve formě elektronkového nebo krystalového zesilovače; někdy se jim říká filtry aktivních prvků.
Pro komplexní charakterizaci činnosti filtru je nutné znát jeho elektrické charakteristiky, které zahrnují frekvenční závislosti útlumu, fázového posunu a charakteristické impedance.
Nejlepší filtr je ten, který s minimálním počtem prvků má:
- maximální strmost charakteristiky útlumu;
- vysoký útlum v dorazovém pásmu;
- minimální a konstantní útlum v propustném pásmu;
- maximální stálost charakteristické impedance v propustném pásmu;
- lineární fázová charakteristika;
- možnost jednoduchého a hladkého nastavení šířky pásma a jeho šířky;
- stálost charakteristik nezávislá na: napětích (proudech) působících na vstupu filtru, okolní teplotě a vlhkosti, jakož i vlivu vnějšího elektrického a magnetického rušení;
- schopnost pracovat v různých frekvenčních rozsazích;
- Zároveň by rozměry, hmotnost a náklady na filtr měly být minimální.
Bohužel neexistuje jediný elementární typ filtru, který by svými vlastnostmi splňoval všechny tyto požadavky. Proto se v závislosti na konkrétních podmínkách používají takové typy filtrů, které svými vlastnostmi nejlépe vyhovují technickým požadavkům. Velmi často je nutné používat filtry složitých obvodů skládajících se z elementárních vazeb různých typů.
Nejběžnější typy filtrů
Na Obr. Obrázek 1 ukazuje schéma jednoduchého filtru ve tvaru L s induktorem L a kondenzátorem C zapojeným mezi přijímač r pr a usměrňovač B.
Střídavé proudy všech frekvencí narážejí na značný odpor induktoru a paralelně zapojený kondenzátor prochází paralelní větví zbytkové vysokofrekvenční proudy. Díky tomu se výrazně sníží zvlnění napětí na zátěži r.
Lze také použít filtry sestávající ze dvou nebo více podobných jednotek. Někdy se používají zjednodušené filtry s odpory místo induktorů.
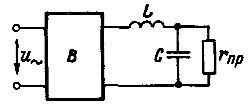
Rýže. 1. Nejjednodušší vyhlazovací elektrický filtr ve tvaru L
Pokročilejší jsou rezonanční filtry, které využívají rezonanční jevy.
Při sériovém zapojení induktoru a kondenzátoru, kdy fw L = 1/(k w C), bude mít obvod nejvyšší vodivost (aktivní) na frekvenci fw a dosti vysoké vodivosti ve frekvenčním pásmu blízkém rezonančnímu. Tento obvod je jednoduchý pásmový filtr.
Při paralelním zapojení induktoru a kondenzátoru bude mít takový obvod nejnižší vodivost na rezonančním kmitočtu a relativně nízkou vodivost ve frekvenčním pásmu blízkému rezonančnímu. Takový filtr je bariérovým filtrem pro určité frekvenční pásmo.
Pro zlepšení výkonu jednoduchého pásmového filtru můžete použít obvod (obr. 2), ve kterém jsou k přijímači paralelně připojeny induktor a kondenzátor. Takový obvod je také naladěn do rezonance na kozí frekvenci a představuje velmi vysoký odpor pro proudy zvoleného frekvenčního pásma a mnohem menší odpor pro proudy jiných frekvencí.
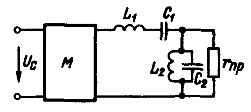
Rýže. 2. Obvod jednoduchého pásmového elektrického filtru
Podobný filtr lze použít v modulátorech, které produkují modulované kmity o určité frekvenci. Modulátor M je napájen napětím Uc nízkofrekvenčního signálu, které se převádí na modulované vysokofrekvenční kmity a filtr volí napětí o požadované frekvenci, které je přivedeno na zátěž r pr.
Předpokládejme například, že obvodem protéká nesinusový střídavý proud a je nutné eliminovat velmi velké třetí a páté harmonické z proudové křivky přijímače. Poté zapojíme dva obvody do série v obvodu, naladěné na rezonanci pro třetí a pátou harmonickou (obr. 3, a).
Odpor levého obvodu, naladěného na rezonanci pro frekvenci 3 W, bude pro tuto frekvenci velmi vysoký a pro všechny ostatní harmonické malý; podobnou roli hraje i správný obvod, laděný do rezonance pro frekvenci 5w. Proto proudová křivka inp přijímače téměř nebude obsahovat třetí a pátou harmonickou (obr. 3,b), které budou filtrem potlačeny.
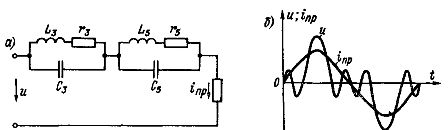
Rýže. 3. Obvod s rezonančními obvody zapojenými do série, laděnými do rezonance pro třetí a pátou harmonickou: a – schéma zapojení; b – křivky napětí a obvodu a proudu inp přijímače
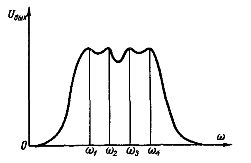
Rýže. 4. Křivka napětí na výstupu pásmového filtru
V některých případech se používají i pokročilejší pásmové filtry a také řezací filtry, které přenášejí nebo nepřenášejí vibrace, a to již od určité frekvence. Takové filtry se skládají z článků ve tvaru T nebo U.
Princip funkce filtrů spočívá v tom, že ve frekvenčním propustném pásmu, např. pásmového filtru, dochází k rezonanci na n+1 frekvencích, kde n je počet spojů. Křivka Uout = f( w) pro takový filtr, složený ze tří článků, je na Obr. 4. Rezonance se vyskytuje na frekvencích w1, w2, w3 a w4.
Telegramový kanál pro ty, kteří se chtějí každý den učit nové a zajímavé věci: Škola pro elektrikáře
Pokud se vám tento článek líbil, sdílejte odkaz na něj na sociálních sítích. Velmi to pomůže rozvoji našeho webu!
Nenechte si ujít aktualizace, přihlaste se k odběru našich sociálních sítí:

Kalmanův filtr: složitá matematika jednoduchými slovy
Pokud vyvíjíte roboty nebo autopiloty, pak jste pravděpodobně již slyšeli o Kalmanově filtru. Ale co to je a jak to funguje?
Obvykle se při seznamování s Kalmanovým filtrem běžný člověk setká s mnoha složitými vzorci. V tomto článku si tyto matematické pojmy jednoduše vysvětlíme na konkrétních příkladech.

Obrázek 1 – Nesrozumitelné vzorce
Co je to Kalmanův filtr?
Kalmanův filtr je matematický algoritmus, který vám umožňuje odhadnout stav systému na základě neúplných, zašuměných informací. Může to být jakýkoli systém, který je třeba monitorovat nebo řídit (robot, dron, auto nebo proces na výrobní lince).
Kalmanův filtr byl vyvinut Rudolfem Kalmanem v roce 1960 a stal se široce používaným v mnoha oblastech, včetně letectví, automobilového průmyslu, lékařství a dokonce i domácích spotřebičů. Umožňuje získat přesnější hodnocení stavu systému než pouhé čtení dat ze senzorů.

Obrázek 2 – Rudolf Kalman
Jak funguje Kalmanův filtr?
Kalmanův filtr funguje na principu predikce a úpravy. Nejprve předpovídá budoucí stav systému na základě aktuálního stavu a informací o jeho pohybu. Tuto předpověď pak upraví na základě nových informací ze senzorů.
Jak lze předpovědět budoucnost nebo pochopit současný stav systému? Nejprve se podívejme na nezbytnou terminologii z teorie pravděpodobnosti.
1. Něco málo z teorie pravděpodobnosti:
Pokud změříte množství mnohokrát, skončíte s mnoha body rozptýlenými kolem tohoto množství. Taková měření jsou ve většině případů popsána zákonem normálního rozdělení a funkce, která je popisuje, se nazývá Gaussova křivka (Gaussova).
Obrázek ukazuje zákon normálního rozdělení náhodné veličiny X ve formě histogramu. Vodorovná osa ukazuje naměřenou hodnotu a svislá osa ukazuje počet měření spadajících do intervalu a normalizovaných podle výšky tak, aby plocha pod grafem byla rovna jedné.
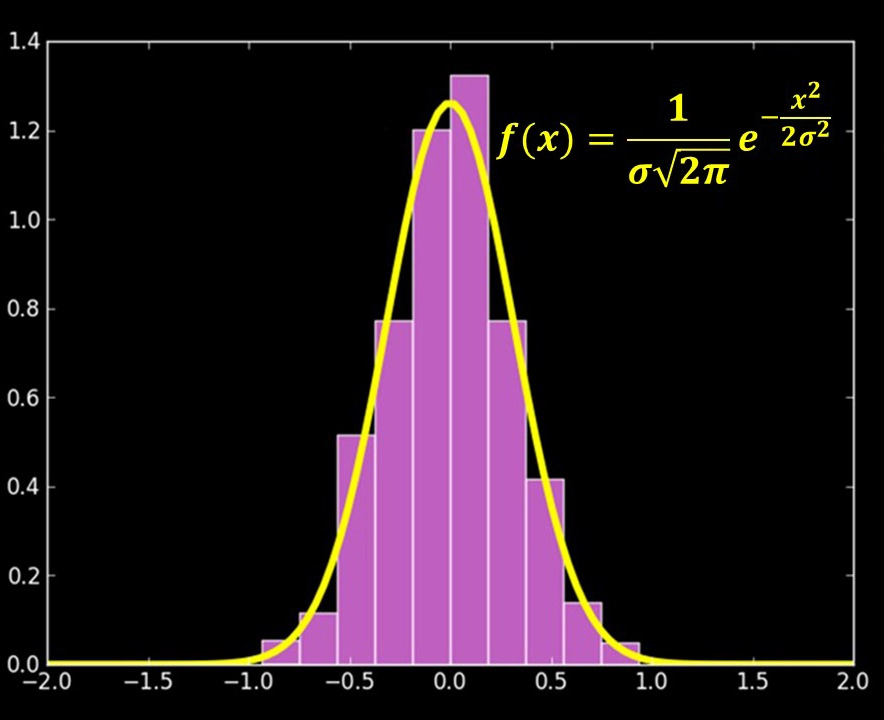
Obrázek 3 – Příklad zákona o normálním rozdělení
To se děje tak, že Gaussova křivka představuje funkci rozdělení pravděpodobnosti.
Gaussian má dva hlavní parametry:
– matematické očekávání (uprostřed grafu, na obrázku 3 je nula)
– standardní odchylka (sigma, σ ).
V závislosti na matematickém očekávání a sigmě mají Gaussiany různé tvary a „středy“ (obrázek 4).
Čím menší je sigma, tím vyšší a tenčí je Gaussian. V tomto případě je plocha pod Gaussiánem, která popisuje rozložení veličiny, vždy stejná a rovná se jednotě.

Obrázek 4 – Tvar Gaussianu v závislosti na jeho parametrech
Jako parametr je standardní odchylka (sigma, σ ) souvisí s Gaussovým?
Pro jakýkoli Gaussian platí segment ± σ obsahuje 68,3 % plochy pod grafem, pro interval ±3 σ tato hodnota je již 99,7 %. To znamená, že 99,7 % všech měření leží mezi minus třemi a třemi sigma.
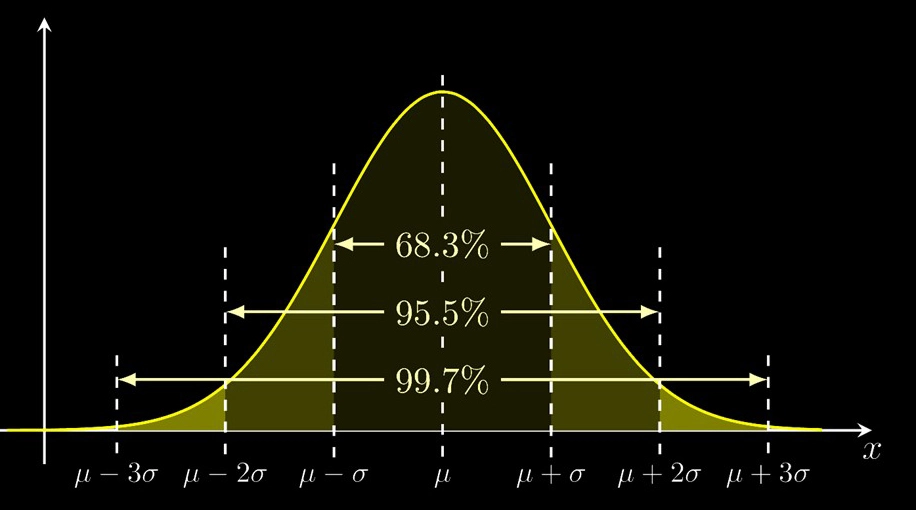
Obrázek 5 – Počet měření spadajících do různých intervalů
2. Příklad s robotickým vysavačem
Podívejme se na konkrétní příklad, abychom lépe pochopili, jak to funguje.
Řekněme, že máme robotický vysavač, který se pohybuje po místnosti a sbírá prach. Je vybavena senzory, které mu umožňují určit jeho polohu v prostoru a vzdálenost k předmětům (zdi, nábytek). Kvůli šumu a nepřesnosti v datech senzorů však nemůžeme přesně určit polohu robota.
Kalmanův filtr řeší tento problém, jak jsme diskutovali výše, skrz předpověď и oprava .
1) Algoritmus předpovídá nové umístění robota na základě předchozích informací o jeho poloze a rychlosti. Pokud byl například robot v bodě (5, 5) a pohyboval se doprava rychlostí (1, 0), další pozice by měla být (6, 5). Ale kvůli nerovnoměrnému pohybu, rušení na dráze a šumu v senzorech si tím nemůžeme být úplně jisti. Filtr tedy odhadne i chybu své predikce. Nechť je v tomto případě naše předpověď (6, 5) podle souřadnic s odchylkou σ = 0.1 metru.
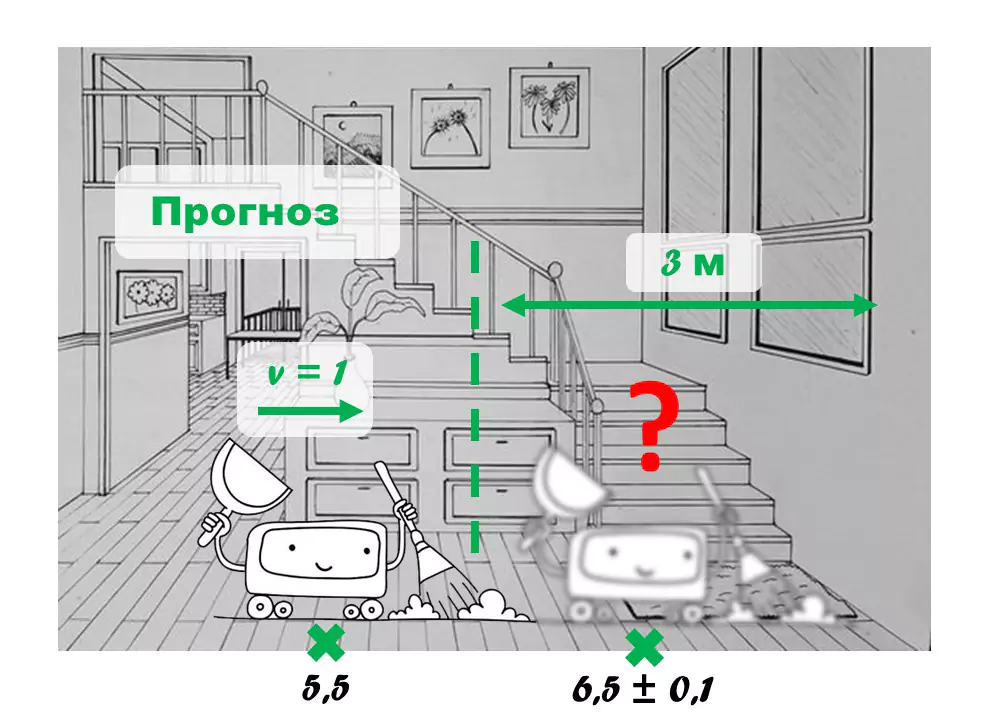
Obrázek 6 – Nová předpověď polohy
2) Algoritmus opravuje předpověď na základě nových informací ze senzorů. Například senzory robota hlásily, že vzdálenost ke zdi je nyní 1,8 metru, zatímco v předchozím časovém kroku byla vzdálenost ke zdi 3 metry. To znamená, že během této doby robot ujel ne 1, ale 1.2 metru. Snímač vzdálenosti má dobrou přesnost, asi několik centimetrů ( σ = 0,02 m ), takže Kalmanův filtr se bude při úpravách více spoléhat na data snímače vzdálenosti.
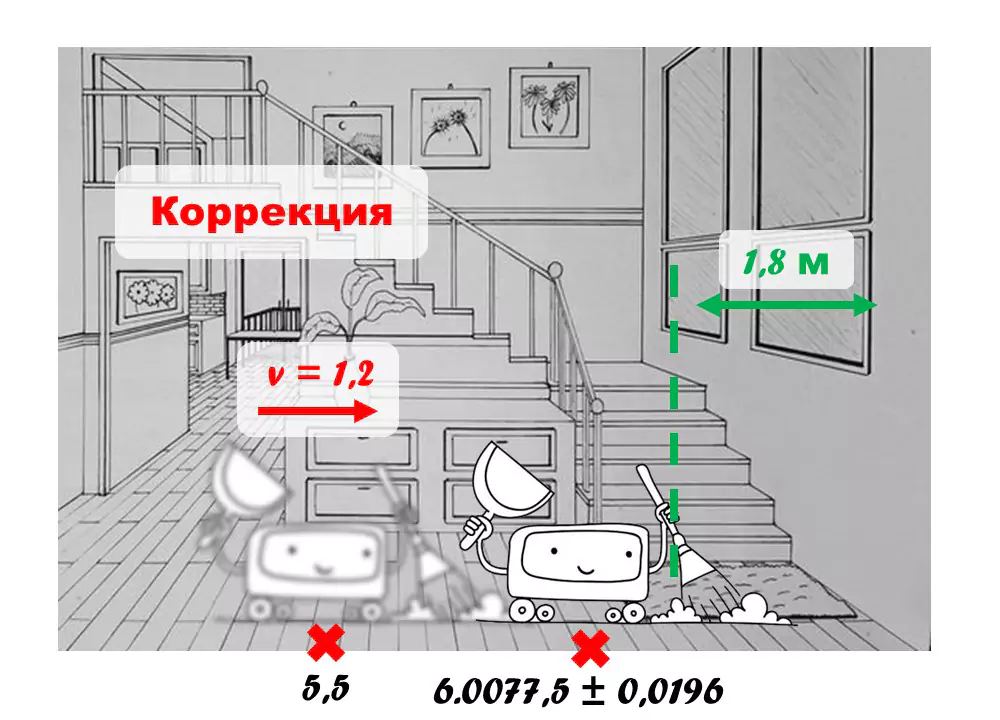
Obrázek 7 – Oprava předpovědi polohy
V tomto případě Kalmanův filtr předpoví, že robot v nové pozici bude mít souřadnice (6.0077,5) s aktualizovanou odchylkou σ = 0,0196 m .
Kalmanův filtr: vzorce a matematika
Zjednodušeně řečeno, Kalmanův filtr umožňuje určit optimální odhad stavu systému s přihlédnutím k dostupným informacím a šumu. Kalmanův filtr je matematický algoritmus a používá vzorce k výpočtu optimálního odhadu stavu systému.
Kalmanův filtr používá dva typy vzorců:
1) Předpovědní vzorec budoucí stav systému na základě předchozích informací o jeho stavu a pohybu:

2) Vyrovnávací vzorec předpověď na základě nových informací ze senzorů:

Další příklad
Analyzujme princip fungování Kalmanova filtru na příkladu jednorozměrného letu letadla.
Letadlo letí vpravo podél osy x s rychlostí v. Řekněme, že známe jeho souřadnice v předchozím časovém okamžiku
x i-1 s chybou (sigma) σ i-1 .
Pro výpočet souřadnic v aktuálním čase se nejprve provede krok predikce.
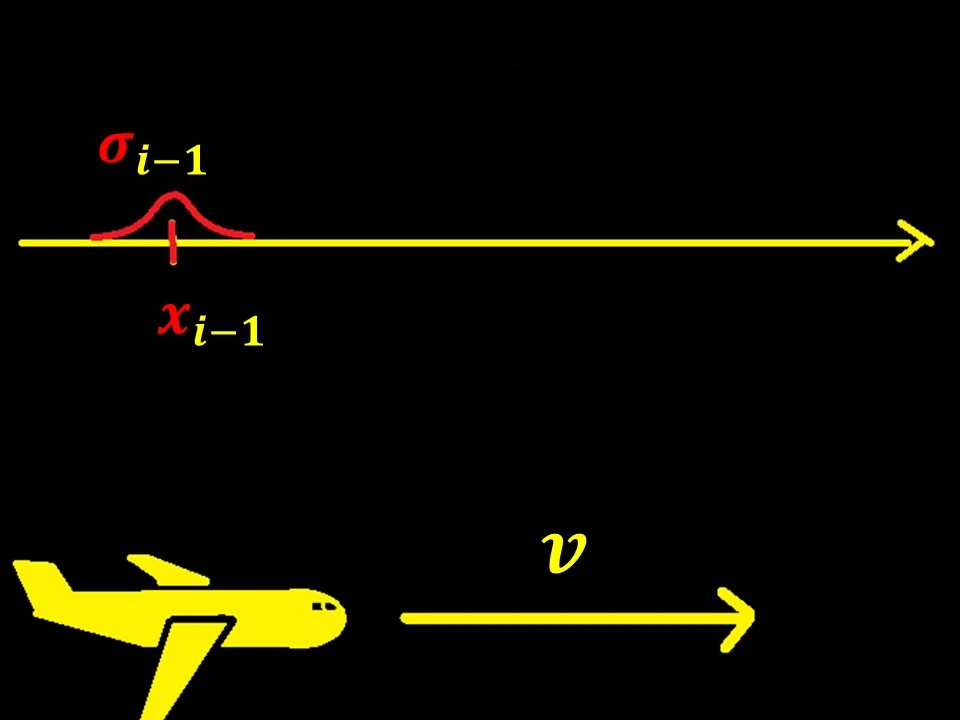
Obrázek 8 – Let jednorozměrného letadla
Pomocí známého kinematického modelu (v tomto případě se jedná o přímočarý rovnoměrný pohyb) je predikce souřadnice ͡x i a předpovídání chyby při určování této souřadnice ͡σ i podle minulých údajů.
Chybová předpověď se získá umělým přidáním chyby q při každé iteraci.
V případech, kdy z toho či onoho důvodu nenastane krok korekce, musí krok predikce neustále zvyšovat chybu při určování stavu kvůli chybám modelu, nelinearitě pohybu a chybám ve výpočtu.
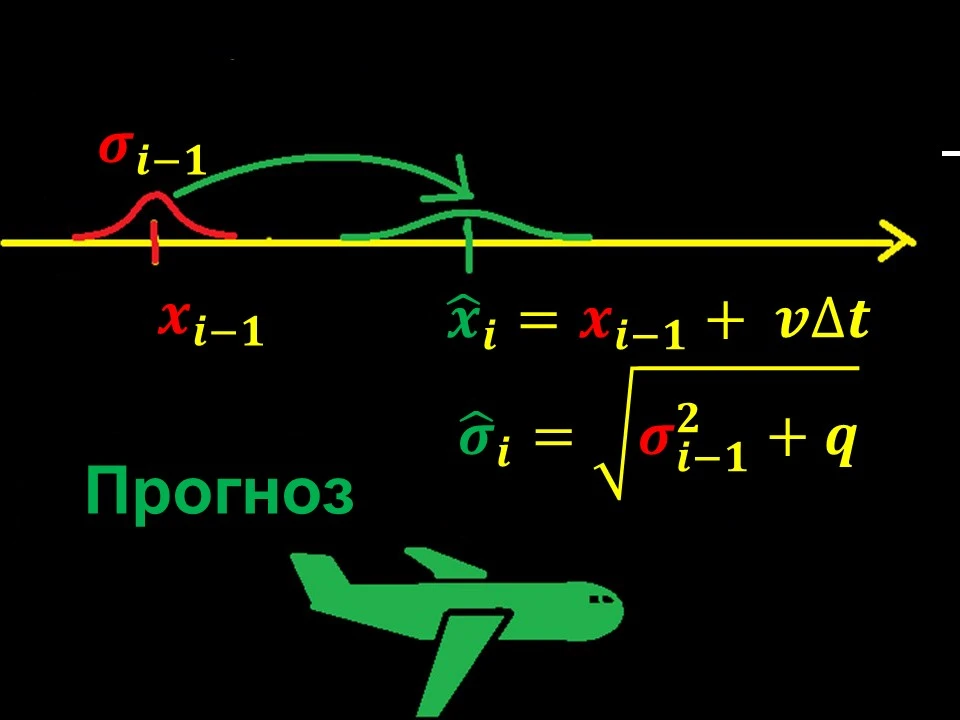
Obrázek 9 – Predikce polohy letadla
Kromě predikce při každé iteraci známe i naměřené souřadnice letadla r.
To lze provést například pomocí přijímače GPS. Ovšem samotné měření souřadnic r nepřesné a má svou vlastní chybu σ r .
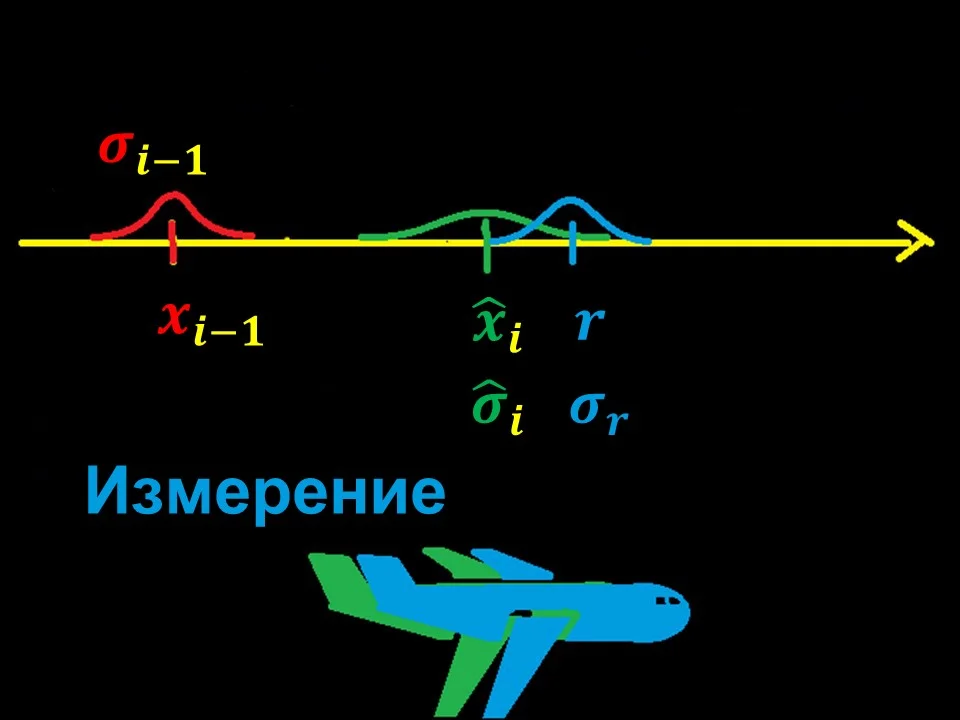
Obrázek 10 – Naměřené souřadnice letadla
Posledním krokem je oprava.
V tomto kroku dříve předpovězená souřadnice ͡x i objasněno měřením r. Tím přesněji známe naši naměřenou souřadnici r (tj. čím menší je sigma σ r ) tím bližší je konečná souřadnice x i bude k měření r. A naopak, čím horší je přesnost GPS přijímače, tím více se budeme spoléhat na předpovězenou souřadnici ͡x i
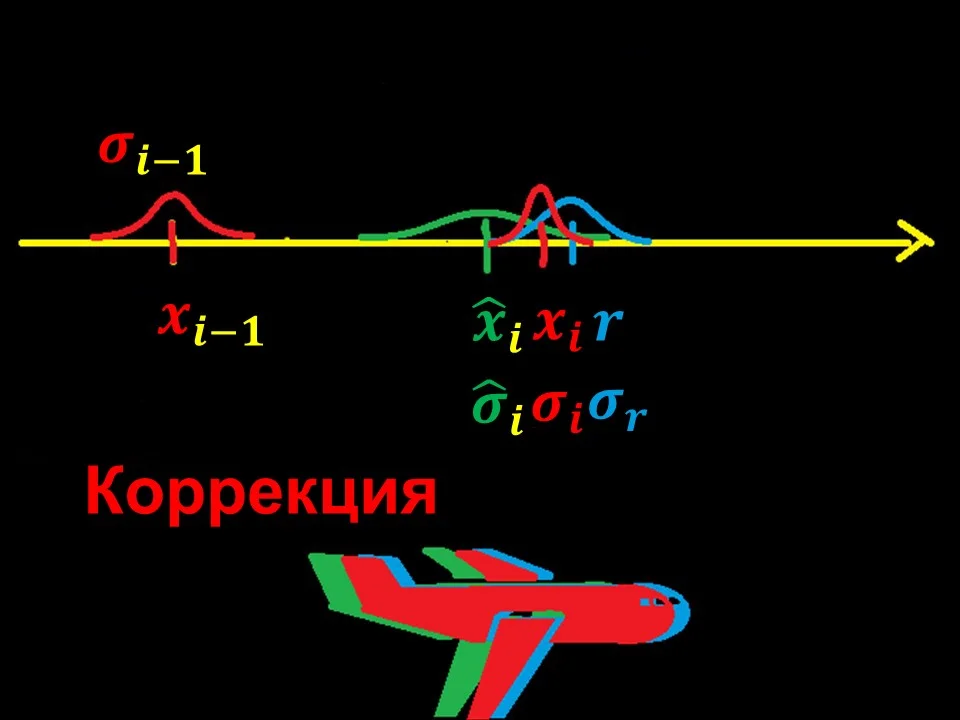
Obrázek 11 – Korekce polohy letadla
Koeficient je přímo zodpovědný za výpočet konečné souřadnice К, takzvané jádro Kalmanova filtru.
Jestliže K je blízká nebo rovna nule, pak konečná souřadnice x i se bude blížit předpokládané hodnotě ͡x i . Pokud K se blíží jednotě, tedy konečné hodnotě x i bude blíže k měření r.

Obrázek 12 – Výpočet výsledné souřadnice
Podívejme se blíže na násobení dvou Gaussovců ve fázi korekce.
Předpokládejme, že odhad chyby polohy je velký (sigma je relativně velká, graf je „široký a zploštělý“).
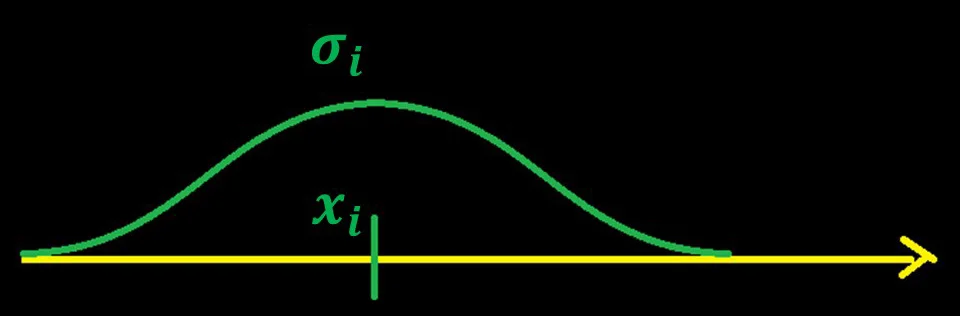
Obrázek 13 – Odhady chyb polohy
A odhad chyby měření je naopak menší (sigma je menší, graf je vyšší a „užší“).
Připomínáme, že plocha pod každým grafem je stejná a rovná se jedné.
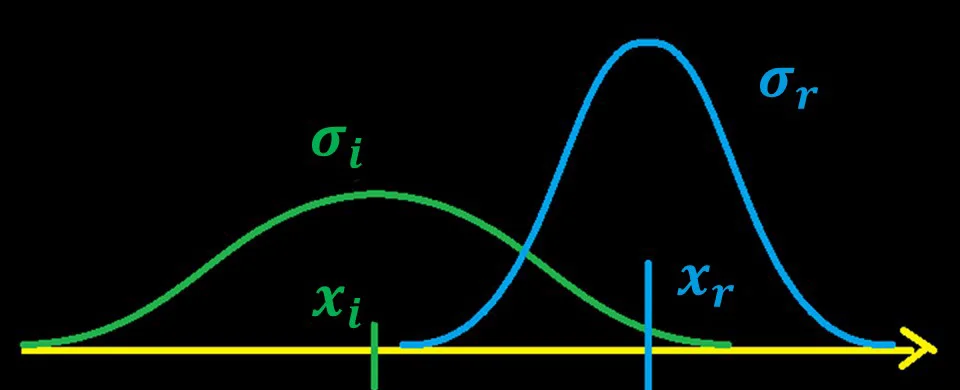
Obrázek 14 – Odhady chyby polohy a chyby měření
Pak bude výsledek „normalizovaného násobení“ (vynásobení dvou Gaussiánů a pak zmenšení grafu na jednotku plochy pod ním) dvou Gaussiánů takový, jak je znázorněno na obrázku 15.
V tomto případě je výsledek korekce blíže měření x r , což je způsobeno menší sigmou σ r . Výsledná sigma bude menší než kterákoli z původních.
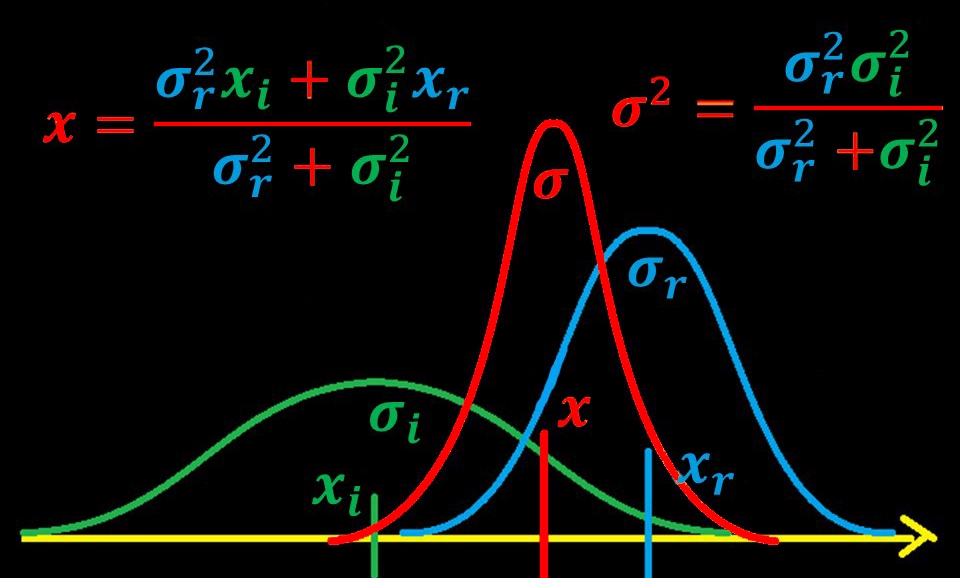
Obrázek 15 – Normalizované násobení Gaussiánů
Nyní, když uživatel narazí na Kalmanův filtr a jeho „děsivé“ vzorce, má méně otázek.

Obrázek 16 – Nepříliš nesrozumitelné vzorce
Závěr
Kalmanův filtr je výkonný algoritmus, který se používá v různých oblastech včetně robotiky, automobilového průmyslu, leteckého inženýrství a dalších. Umožňuje určit optimální vyhodnocení stavu systému s přihlédnutím k šumu v datech ze senzorů a předchozím informacím o stavu systému.
Ačkoli se matematika Kalmanova filtru může zdát složitá, její koncept lze vysvětlit jednoduchými slovy. Je důležité si uvědomit, že Kalmanův filtr je nástroj, který může pomoci zpracovat data a zlepšit přesnost předpovědí v různých aplikacích.
Přihlaste se k odběru našeho kanálu Telegram: https://t.me/mplab
Na tomto kanálu zveřejňujeme: případy (naše články a výzkumy); informace o produktech (úpravy a nové položky); Odpovídáme na časté dotazy a další oznámení.
Přečtěte si také

Navigační výpočetní technika pro zemědělské stroje

Nastavení a připojení základnové stanice
O nás
Vývoj a výroba inerciálních navigačních systémů na bázi MEMS.
Laboratoř Microdevices byla založena v roce 2012, je rezidentem SEZ a má certifikát QMS GOST R ISO 9001-2015.
















