Kdo přišel s kořeny?

Проектная работа

Cíl práce: 1. Co znamená kořenový znak a odkud pochází?

1.Co znamená kořenový znak a odkud pochází?
2. Seznamte se s definicí odmocniny.
3. Řekněte, kdo objevil druhou odmocninu.
4. Zjistěte, kde se používají odmocniny.
5. Závěr.

Úloha Uvažujme jednoduchý problém z hlediska geometrie

Uvažujme jednoduchý problém z geometrického hlediska. Rozdělme čtverec o ploše 4 na čtyři jednotkové čtverce a do každého z nich nakreslete úhlopříčku, jak je znázorněno na obrázku. Výsledkem je další, vnitřní čtverec, jehož plocha se rovná polovině plochy velkého čtverce, tedy 2. Tyto elementární argumenty nás přivedly k velmi důležitému faktu – existenci čtverce o ploše 2. Nyní odpovězte: jaká je délka strany tohoto čtverce?

Kdo je zodpovědný za objev druhé odmocniny?

Pythagorejci zjistili, že úhlopříčka čtverce je nesouměrná s jeho stranou, nebo v moderním jazyce, že druhá odmocnina ze dvou je neracionální číslo. O době a okolnostech tohoto pozoruhodného objevu je s jistotou známo jen málo, ale tradičně se připisuje jeho autorství Hippasou z Metapontu. Podle různých verzí ho za tento objev Pythagorejci buď zabili, nebo vyhnali a obvinili ho ze zničení hlavní pythagorejské doktríny, že „všechno je (přirozené) číslo“. Proto se odmocnina ze dvou někdy nazývá pythagorejská konstanta, protože pythagorejci dokázali, že je iracionální, čímž objevili existenci iracionálních čísel.

Kořenové znamení, co to znamená a odkud pochází?

Aritmetický kořen pochází z latinského slova radix – kořen, radikalis – radikál
Počínaje 13. stoletím italští a další evropští matematici označovali kořen latinským slovem radix
(zkráceně r). V roce 1525 se v knize H. Rudolfa „Rychlý a krásný výpočet s využitím dovedných pravidel algebry“ objevilo označení V pro druhou odmocninu a VVV pro odmocninu krychlovou. V roce 1626 zavedl holandský matematik A. Girard označení V, V atd., které brzy nahradilo znak r, s vodorovnou čarou umístěnou nad radikálním výrazem. Moderní zápis kořene se poprvé objevil v knize René Descartes Geometry, vydané v roce 1637.

Co je to druhá odmocnina?

Druhá odmocnina nezáporného čísla а je nezáporné číslo, jehož druhá mocnina se rovná a.

ČTĚTE VÍCE

Proč línají krevety?

Vlastnosti odmocnin. Příklady: =6 =6

Úkol

Kde se používá druhá odmocnina?

Odmocnina se používá hlavně v matematice a fyzice ke zjednodušení složitých mocninných funkcí, nerovnic a rovnic. Dokonce i ve starověku lidé jednoduše potřebovali vypočítat druhou odmocninu. Mnozí se zabývali zemědělstvím a rozdělením území na čtverce, bez odmocniny nedokázali nic vypočítat. Proto bylo kořenové znamení zavedeno lidskou nutností, protože lidé v šestnáctém století znali oblast a potřebovali vypočítat stranu čtverce. Proto byla zavedena odmocnina, kterou používáme dodnes. A teď to často potřebujeme. Připomeňme si Pythagorovu větu Co o ní víme? Druhá mocnina přepony se rovná součtu čtverců nohou v pravoúhlém trojúhelníku. A pokud potřebujeme vypočítat stranu čtvercového pozemku o velikosti 100 metrů čtverečních, co použijeme? Samozřejmě odmocnina. A pak to pro nás bude snadné. Druhá odmocnina ze 100 je 10. Ukazuje se, že naše strana webu je 10 metrů.

Závěr: Naprostý počet problémů o prostorových formách a kvantitativních vztazích v reálném světě spočívá v řešení různých typů rovnic.

Naprostý počet problémů o prostorových formách a kvantitativních vztazích v reálném světě spočívá v řešení různých typů rovnic. Zvládnutím způsobů jejich řešení nacházíme odpovědi na různé otázky z oblasti vědy a techniky.

Použité zdroje: Dorofeev

Použité zdroje:

Dorofeev G.V., Suvorova S.B., Bunimovich E.A. atd. Algebra. 8. třída. Učebnice.
5. vyd. – M.: 2010. – 288 s.
http://images.yandex.ru
http://animashky.ru/index/0-6

Materiály na této stránce jsou převzaty z otevřených zdrojů nebo zveřejněny uživatelem v souladu s dohodou o nabídce webu. Můžete nahlásit zneužití.

Tato hliněná tabulka, vyrobená kolem roku 1800-1600 před naším letopočtem, ukazuje, že staří Babyloňané byli schopni aproximovat druhou odmocninu ze dvou s přesností 99,9999 %.

Nejprve si dešifrujeme samotné znamení. Nese označení YBC 7289 (zkratka pro „Yale Babylonian Collection Item 7289“). Na štítku je zobrazen čtverec, jeho úhlopříčka a čísla napsaná vedle něj. Zde je stylizovaná verze z knihy Epizody z rané historie matematiky Tapeta na plochu Asgera.

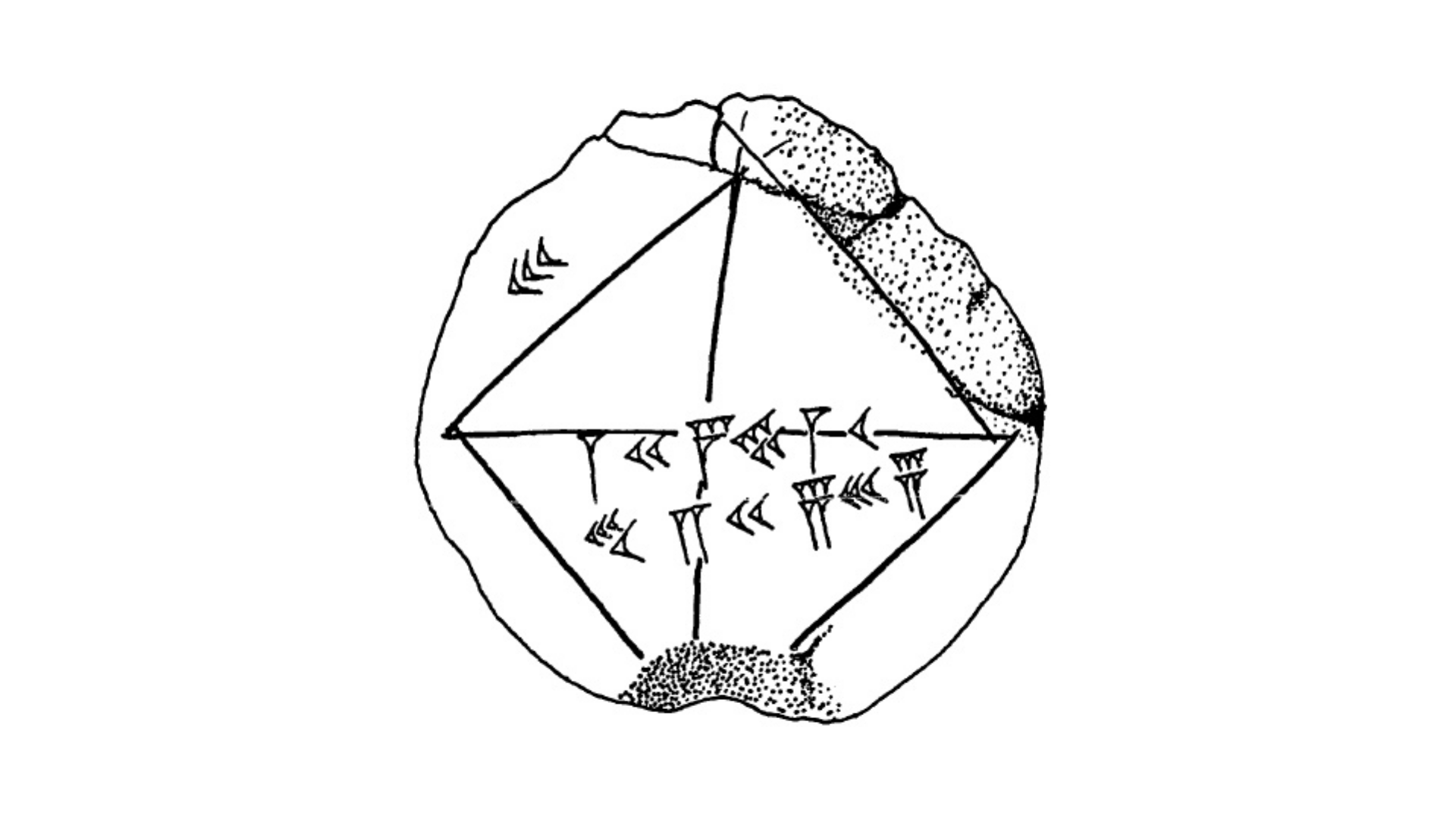
Jak vyplývá z Pythagorovy věty, délka úhlopříčky jednotkového čtverce je √2. Podívejme se na symboly!

Tabulka obsahuje čísla zapsaná ve formě babylonských klínopisných číslic. Znamená to 1, 24, 51 a 10.

ČTĚTE VÍCE

Jak dlouho žijí Killifish?

Protože Babyloňané používali číselný systém se základním 60 (také nazývaný šestinedělí), číslo 1,24 51 10 v desítkové soustavě znamená 1,41421296296.

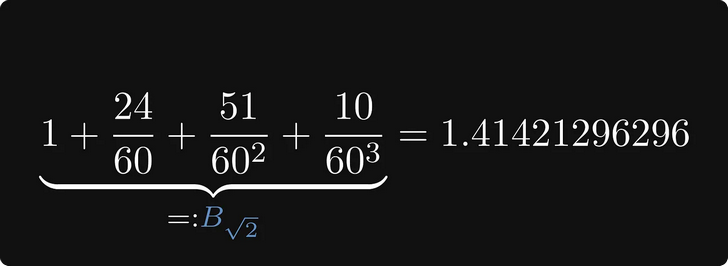
To je stejné jako √2 na šesté desetinné místo, což je 99,9999% přesnost!

Přesnost výpočtů je úžasná. Zkuste to znovu vytvořit bez kalkulačky, na papíře, není to tak snadné!

A my vám prozradíme, jak se jim to povedlo.

Nyní budu předstírat, že jsem kouzelník: nejprve ukážu algoritmus a pak odhrnu závěs a vysvětlím to.

Začneme výběrem čísla x₀ mezi 1 a √2. Vím, že to vypadá náhodně, ale neuspěchejme to. Toto číslo může být například 1,2, což by byla naše první aproximace.

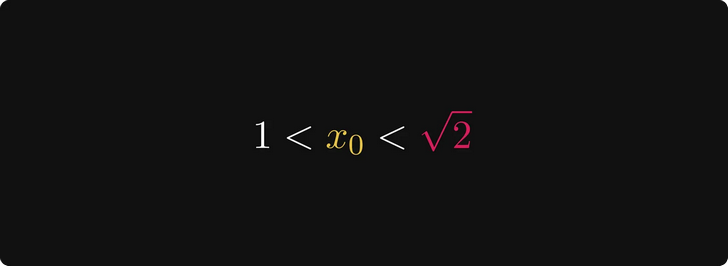
Na základě toho je 2/x₀ větší než √2.

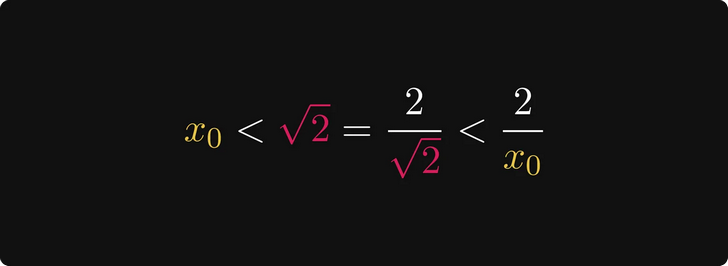
Proto interval [x₀, 2/x₀] zahrnuje √2.

Z toho vyplývá, že střed intervalu [x₀, 2/x₀] je přesnější aproximací hodnoty √2. Jak můžete vidět na obrázku níže, je výrazně lepší!

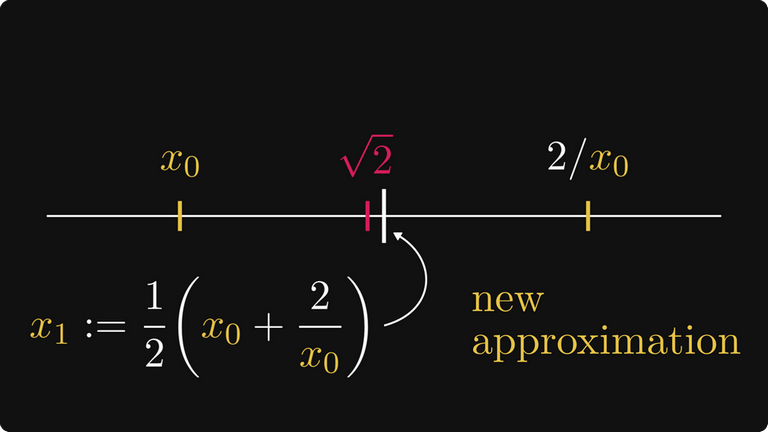
Z toho určíme x₁.

Při rozvíjení tohoto tématu můžeme určit aproximační sekvenci tím, že vezmeme středy takových intervalů.

Zde je několik prvních termínů sekvence. I třetí termín je již překvapivě dobrým přiblížením.

Pokud tato čísla vyneseme na bodový graf, po několika krocích prakticky potřebujeme mikroskop, abychom viděli rozdíly od √2.

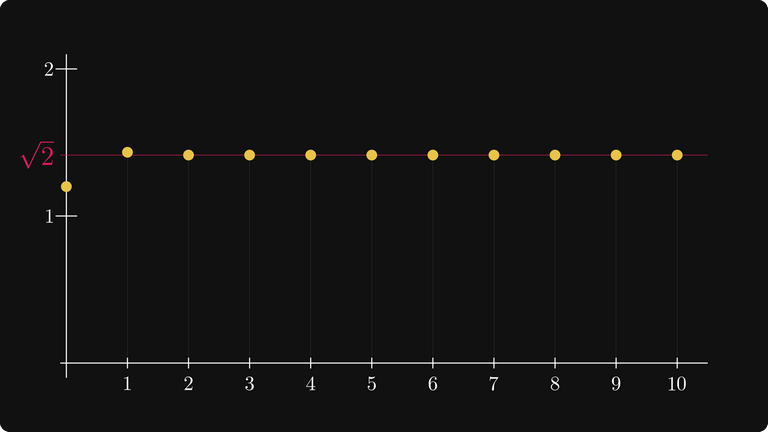
Jak můžete vidět, toto konverguje k √2 extrémně rychle.

Chyba v babylonské aproximaci

Chyba mezi touto aproximací a hodnotou √2 je jednoduše definována jako vzdálenost mezi nimi, měřená absolutní hodnotou jejich rozdílu. Například chyba našeho prvního odhadu e₀ je dána takto:

Bez ohledu na to, jak malé nebo velké je e₀, můžeme jej použít k odhadu následných chyb.

Pojďme si udělat nějakou algebru a uvidíme, jak e₀ souvisí s e₁! Nejprve vyjádřeme e₁ jako zlomek.

Potom, protože jsme zvolili x₀ větší než jedna, můžeme to vyjádřit pomocí e₁. Protože čitatel e₀ je na druhou, je náš problém jednoduchý.

Opakováním těchto argumentů zjistíme, že konvergence je velmi rychlá, dokonce rychlejší než exponenciální!

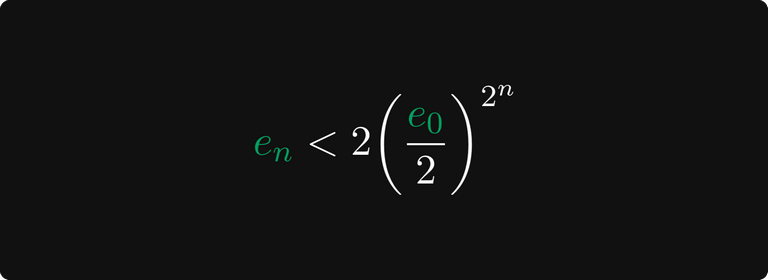
Měli Babyloňané štěstí, nebo trefili hřebíček na hlavičku?

Vlastně je to ten druhý. Je čas zvednout oponu!

ČTĚTE VÍCE

Kam sumec vzal dívku?

Přeformulujme problém aproximace druhé odmocniny ze dvou. Místo hodnocení funkce f (x) = √x v daném bodě zkusme najít kořen (kladný) f(x) = x² – 2. (Což, jak se ukázalo, se také rovná √2.)

Existuje zobecněná metoda řešení takového problému? Ano, toto je Newton-Raphsonova metoda. Abychom ukázali, jak to funguje, pojďme si přiblížit kořen f (x).

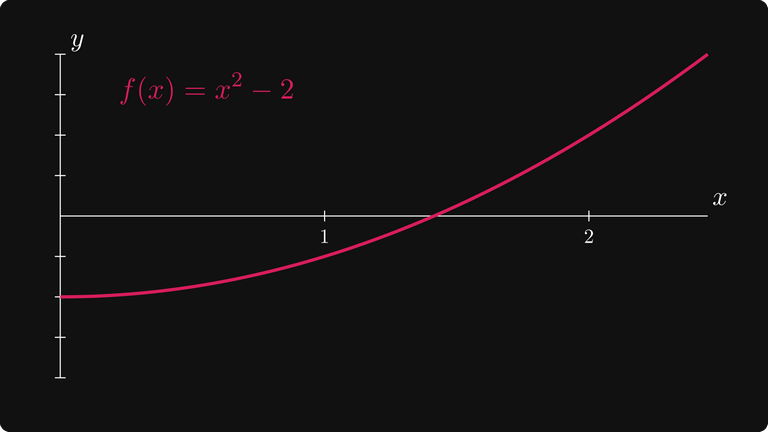
Graf f(x) = x² – 2

Jak se můžeme posunout od našeho původního odhadu x₀ ke kořenu?

Můžete například sledovat směr tečny a zjistit, kde protíná osu X. Protože úhel tečny je určen derivací, lze tento průsečík okamžitě vypočítat. Ukážu vám, jak na to.

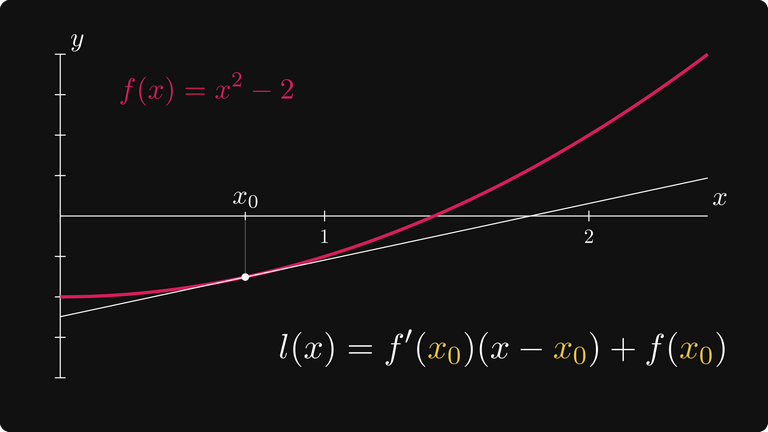
Rovnice tečny je dána následovně.

Když to vyrovnáme nule a vyřešíme to, dostaneme bod, ve kterém tečna protíná osu X.

Takže výběrem dalšího odhadu x₁ jako tohoto průsečíku získáme (doufejme) přesnější aproximaci.

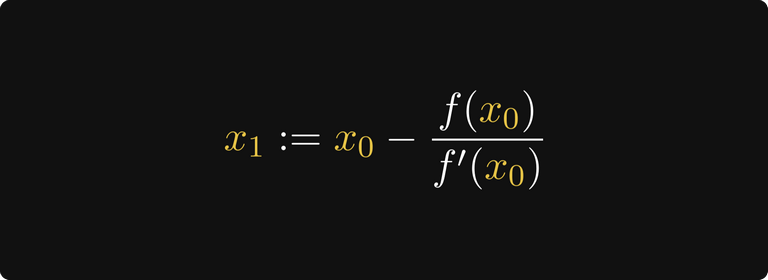
To je vše! Na základě této myšlenky můžeme definovat rekurzivní sekvenci.

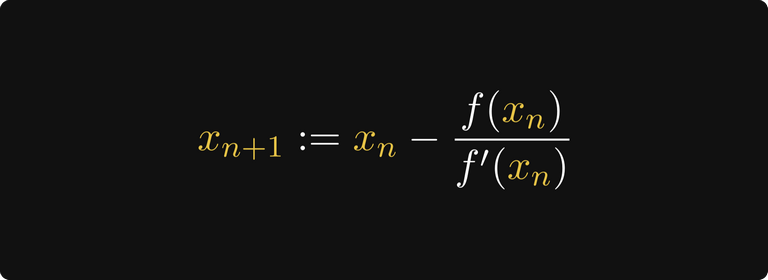
Toto se nazývá Newton-Raphsonova metoda. Zde je další krok. Jak vidíte, třetí krok je téměř na √2.

Zůstává jedna důležitá otázka: byla tato metoda používaná Babyloňany? Ano, a tady je důvod.

Newton-Raphsonova metoda a babylonský algoritmus

V předchozím příkladu jsme se rozhodli najít kořen f(x) = x² – 2. Pojďme najít explicitní vzorec pro rekurzivní posloupnost danou Newton-Raphsonovou metodou. Jeho derivace se snadno spočítá, takže jsme připraveni.

S trochou algebry můžeme dojít k nepříliš překvapivému závěru.

Babylonský algoritmus je proto speciálním případem Newton-Raphsonovy metody!

Pamatujeme si, že konvergence je v tomto konkrétním případě extrémně rychlá. Platí to obecně? Pokud budeme mít štěstí.

Rychlost konvergence

Aniž bychom zacházeli do podrobností, konvergence a její rychlost závisí na místním chování funkce.

Například pokud f (x) je dvakrát diferencovatelný, pak chybový termín pro nprvek lze popsat pomocí derivací a čtverce (n-1)-tá chyba.

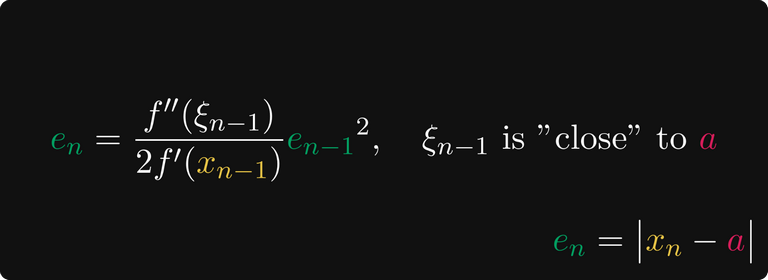
(Pokud vás zajímají podrobnosti, Wikipedia má důkaz.)

Zejména, pokud se deriváty “dobře chovají” (to znamená, že první derivace je oddělena od nuly a druhá derivace je omezená), pak je míra konvergence kvadratická.

Pokud se funkce “chová dobře”

Kvadratická konvergence platí nejen pro nalezení druhé odmocniny ze dvou aproximací kladné odmocniny f(x) = x² – 2, ale také pro širokou škálu funkcí.

ČTĚTE VÍCE

Jaké barvy vidí ryba?

Omezení

Bohužel ne vše je tak dokonalé. Newton-Raphsonova metoda může v celkem běžných případech způsobit vážné poruchy a má i mnoho nevýhod.

Pokud je například funkce blízko kořene „plochá“, konvergence bude bolestně pomalá. Jeden takový případ je uveden níže.

To se stane, když má kořen velkou zvýšenou nejednoznačnost, to znamená, že derivace jsou rovny nule. Když už mluvíme o derivátech, na rozdíl od druhé odmocniny Babyloňanů může být obtížné je vypočítat, takže tato metoda není použitelná.

Celý proces je navíc velmi závislý na počátečním odhadu: iterace může konvergovat k nesprávnému kořenu nebo dokonce divergovat.

To, že staří Babyloňané byli schopni vypočítat √2 na šesté desetinné místo, je docela překvapivé. Tato přesnost je vysoce respektována, zvláště vezmeme-li v úvahu, že byla dosažena téměř před čtyřmi tisíci lety a výpočty byly prováděny ručně.

Jak se ukázalo, neměli jen štěstí; objevili speciální případ výkonné metody schopné aproximovat kořen široké škály funkcí. Stala se známá jako Newton-Raphsonova metoda.